Diseño de redes verdes y localización de instalaciones
- localización verde
- modelos de localización
- logística
- emisiones de carbono
- problema p-median
- optimización logística
- costos de transporte
- transporte intermodal
- logística sostenible
- cadena de suministro
7.1. Introducción
Las emisiones del transporte representan una gran proporción de las emisiones globales, y el transporte de carga es responsable de una parte relativamente importante de estas emisiones. Las emisiones del transporte pueden reducirse mediante diferentes decisiones logísticas, como cambiar el modo de transporte o modificar la ruta o la carga de los vehículos en la red (ver Capítulo 5 de Blanco y Sheffi (2024) para más información sobre logística verde). Estas decisiones logísticas están fuertemente influenciadas por las políticas de inventario implementadas en una empresa (ver Capítulo 6 de Marklund y Berling (2024) para más información sobre la gestión de inventarios sostenibles). Por ejemplo, permitir un modo de transporte más sostenible, pero más lento, generalmente requeriría aumentar o reubicar el inventario en la cadena de suministro.
Además de las decisiones logísticas y las políticas de inventario, el rendimiento del transporte en términos de costos y emisiones está fuertemente determinado por el diseño de la red. En las redes de distribución, esto se refiere en particular a la ubicación de los centros de distribución u otros centros de transporte, como fábricas o terminales cross-dock. En este capítulo, abordamos el problema de la localización de estos centros de transporte.
El problema logístico que determina la configuración de la entrega de bienes de una empresa es el problema de localización de instalaciones. Este problema consiste en determinar la ubicación de un conjunto de instalaciones (por ejemplo, fábricas, terminales cross-dock, centros de distribución) dentro de un espacio físico, de manera que toda la demanda de los clientes sea atendida por al menos una instalación y que el costo total del transporte sea minimizado. Aunque la literatura sobre localización de instalaciones está bien desarrollada y es extensa, en este capítulo nos enfocamos en una variante de este problema que incluye específicamente las emisiones de carbono del transporte en la formulación. Nos referimos a los problemas de localización cuyo objetivo es minimizar las emisiones de CO₂ del transporte como problemas de localización de instalaciones verdes.
Al limitar el alcance a las emisiones de fuentes móviles (es decir, el transporte), no consideramos las emisiones de fuentes estacionarias que podrían verse afectadas por la decisión de localización. Sin ser exhaustivos, estas pueden incluir:
– Emisiones en el centro de distribución. Estas están relacionadas con el consumo de energía del centro de distribución. En la mayoría de los casos, esto se debe a la electricidad utilizada para la iluminación, la automatización y la refrigeración. Potencialmente, pueden existir economías de escala relacionadas con el diseño de la red. Datos del sector sugieren que, en la mayoría de las redes de distribución, las emisiones en el centro de distribución representan menos del 10% de las emisiones logísticas totales.
– Disponibilidad de fuentes de energía locales. En particular, para operaciones con alto consumo de energía, la disponibilidad de energía renovable local puede tener un impacto significativo en las emisiones de la cadena de suministro. Por ejemplo, ubicar una planta de aluminio en una zona donde haya electricidad geotérmica disponible podría reducir las emisiones totales de carbono de la cadena de suministro, aunque aumente las emisiones del transporte.
Excluir las emisiones de fuentes estacionarias de los modelos discutidos en este capítulo implica que, en la práctica, nos estamos limitando a redes de distribución y a la elección de la ubicación de centros de distribución y terminales cross-dock. Sin embargo, en nuestra discusión utilizamos el término más general "instalación".
Generalmente, las empresas que diseñan sus canales de distribución seleccionan la ubicación de los almacenes y centros de distribución con el objetivo de satisfacer la demanda de los clientes mientras minimizan la distancia (o los costos de transporte). En este capítulo, revisamos algunos modelos que incorporan las emisiones de CO₂ del transporte en la localización de instalaciones sin restricciones de capacidad. Luego, discutimos las soluciones que podemos obtener cuando el número de instalaciones a ubicar está fijado utilizando el problema p-Median. Presentamos análisis y implicaciones gerenciales para la localización de instalaciones verdes. Nuestro interés es determinar si las decisiones de localización obtenidas minimizando costos son diferentes de aquellas obtenidas a partir del modelo de localización de instalaciones verdes.
7.1.1. Localización de Instalaciones y Emisiones de Carbono
Normalmente, las decisiones de localización de instalaciones se toman considerando los costos asociados, que incluyen el transporte (de las instalaciones a los clientes) y la operación de la instalación (producción y almacenamiento). Como se mencionó anteriormente, podemos dividir las principales fuentes de emisiones de CO₂ asociadas con la localización de instalaciones de manera similar: emisiones de fuentes móviles (transporte) y emisiones de fuentes estacionarias (producción, almacenamiento y manejo). Tener más instalaciones reduce las emisiones de CO₂ de fuentes móviles debido a que la distancia entre la instalación y los destinos de los clientes disminuye. Sin embargo, esto aumenta las emisiones de fuentes estacionarias debido al mayor número de instalaciones. Por lo tanto, el desafío en la localización verde de instalaciones es definir el número y la posición adecuados de las instalaciones que atenderán a un conjunto de clientes mientras se minimizan las emisiones totales de CO₂.
Muchos estudios muestran que el transporte y la producción pueden contribuir sustancialmente a las emisiones de CO₂. Por ejemplo, los tres principales sectores que contribuyen a las emisiones en el mundo desarrollado son la generación de electricidad, la manufactura intensiva en energía y el transporte (Agencia Europea del Medio Ambiente, 2018). Mientras que la producción de electricidad y la manufactura intensiva en energía se consideran dentro de los alcances 1 y 2 del inventario de Gases de Efecto Invernadero (GEI), el transporte por parte de los proveedores de servicios se considera dentro de las emisiones de alcance 3 (ver Capítulo 3 de Boukherroub et al. (2024) para más detalles). Las emisiones del alcance 3 a menudo representan la mayor fuente de emisiones de GEI, representando más del 90 % de la huella de carbono de una empresa (World Business Council for Sustainable Development, 2021).
Además, cuando el problema de localización de instalaciones consiste en ubicar centros de distribución en lugar de plantas de producción, normalmente, las emisiones de CO₂ de fuentes móviles son mucho más altas que las de fuentes estacionarias, ya que estas últimas solo incluyen las emisiones generadas en el centro de distribución. Las emisiones del almacenamiento y manejo son sustancialmente menores que las del transporte, hasta 10 veces inferiores para algunos productos (Cholette y Venkat, 2009). Por lo tanto, en este capítulo, nos enfocamos en estudiar la localización de centros de distribución con un énfasis principal en las emisiones de carbono del transporte.
Existen muchas prácticas en la industria para reducir las emisiones de carbono mediante la implementación de prácticas más eficientes y sostenibles en sus operaciones logísticas (por ejemplo, Heineken Sustainability Report, 2013; Groupe Danone, 2014; MIT-EDF, 2013). Sin embargo, pocas han considerado la localización de centros de distribución como una alternativa relevante para reducir las emisiones de CO₂ en el transporte. Por ejemplo, Unilever aumentó el número de centros regionales y los ubicó más cerca de los clientes (Unilever Press Release, 2013).
La localización de instalaciones es fundamental para el funcionamiento eficiente y efectivo de una cadena de suministro; las plantas mal ubicadas pueden resultar en costos excesivos y un bajo nivel de servicio, sin importar qué tan bien se optimicen las decisiones tácticas (por ejemplo, la planificación de rutas de vehículos o la gestión de inventarios) (Daskin et al., 2005). En este capítulo, demostramos que la elección de la localización de instalaciones puede tener un impacto significativo en las emisiones de CO₂ de fuentes móviles en la cadena de suministro. Cabe destacar que los principales factores determinantes de las emisiones de carbono del transporte son la distancia, la carga del vehículo (Greenhouse Gas Protocol Standard, 2015; Smart Freight Centre, 2016) y el número de viajes necesarios para entregar la demanda a cada cliente (Network for Transport Measures, 2022). Cambiar el número y la ubicación de las instalaciones en la red de distribución afecta a todos estos factores.
7.1.2. Compensación entre Costos y Emisiones de Carbono en la Localización de Instalaciones
Los costos de transporte () en los problemas de localización de instalaciones generalmente consideran la demanda () y la distancia (). Estos costos suelen modelarse como una función objetivo basada en la distancia total ponderada por la demanda (, asumiendo un costo constante por unidad de distancia y por unidad transportada (Revelle et al., 2008). Cabe destacar que esta formulación encuentra soluciones óptimas donde las instalaciones están más cerca de las regiones con alta demanda. Sin embargo, para minimizar las emisiones de CO₂ del transporte, pueden ser necesarias soluciones con un enfoque diferente.
Las emisiones de CO₂ del transporte están influenciadas por una variedad de factores relacionados con el tipo de vehículo (por ejemplo, potencia del motor, torque, tipo de combustible, coeficiente de arrastre aerodinámico) y con las características de la operación de entrega (por ejemplo, tipo de carretera, pendiente, velocidad del vehículo, carga) (Akçelik y Besley, 2003). Debido a la falta de información detallada sobre la operación de entrega (pendientes específicas, velocidad, aerodinámica, etc.) durante el proceso de toma de decisiones, las empresas suelen utilizar métodos basados en actividad más agregados para estimar las emisiones de CO₂ (ver Capítulo 3 de Boukherroub et al. (2024) para más información sobre la huella de carbono). Algunos de los métodos basados en actividad más utilizados incluyen GHG Protocol, Global Logistics Emissions Council (GLEC) Framework (Greene y Lewis, 2016) y Metodología desarrollada por la Network for Transport Measures (NTM).
Observamos que un modelo de localización de instalaciones basado en el GHG Protocol o en las metodologías GLEC proporcionaría ubicaciones óptimas idénticas a las soluciones obtenidas mediante la minimización de costos, es decir, las ubicaciones óptimas tenderían a estar más cerca de las regiones con alta demanda. Esto se debe a que estos modelos de estimación multiplican la distancia y la carga por un factor de intensidad de carbono que asume una utilización fija del vehículo, sin considerar explícitamente el número de viajes requeridos para entregar la carga específica. Sin embargo, esto no siempre ocurre cuando se emplea una metodología más detallada como la NTM.
La metodología NTM requiere parámetros más específicos, incluyendo eficiencia del consumo de combustible, distancia recorrida y peso por envío (NTM Road, 2010). La eficiencia del consumo de combustible depende del tipo de camión, el factor de carga y el tipo de carretera.
NTM utiliza la base de datos de European Assessment and Reliability of Transport Emission Models and Inventory Systems, que desarrolló un modelo detallado de emisiones para todos los modos de transporte, proporcionando estimaciones de emisiones coherentes a nivel nacional, internacional y regional (TRL, 2010). El modelo de estimación NTM es:
$$ E = l \left[ d \left( f^e + \left( f^f - f^e \right) \frac{w}{W} \right) \right] , $$
donde:
= emisiones totales en gramos de CO₂
= factor de emisión constante (2621 gramos de CO₂/litro)
fe = consumo de combustible del vehículo vacío (litros/km)
ff = consumo de combustible del vehículo completamente cargado (litros/km)
= capacidad del camión
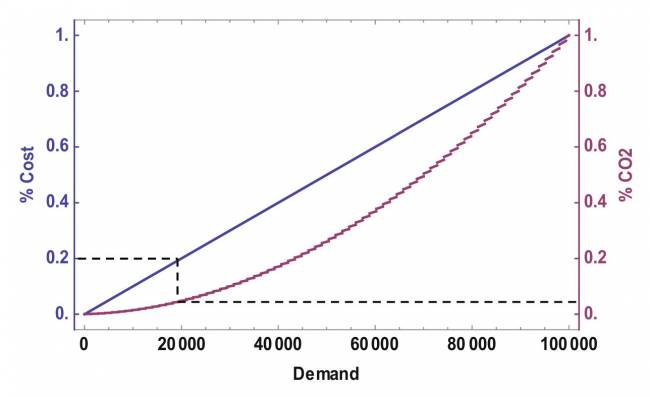
Al comparar los costos de transporte y las emisiones de CO₂, se observa que el efecto de la distancia es lineal en ambas expresiones. Sin embargo, la demanda y la capacidad del camión afectan los costos de transporte de manera diferente a como afectan las emisiones de CO₂. La Figura 7.1 muestra la comparación entre los costos de transporte y las emisiones de CO₂ para diferentes niveles de demanda. Para este ejemplo, utilizamos un camión de 14 toneladas para carreteras urbanas, considerando que 100 unidades de demanda equivalen a 1 tonelada.
Es importante notar que el crecimiento de la demanda no se traduce en un aumento lineal de las emisiones de CO₂, como sí ocurre con los costos. Por ejemplo, una demanda de 20,000 unidades puede aumentar los costos hasta en 20%, mientras que el aumento en las emisiones de CO₂ es de aproximadamente 5%. El gráfico también muestra que un aumento en la demanda impacta las emisiones de CO₂, principalmente cuando este crecimiento implica más viajes.
Debido a estas diferencias en las estructuras de costo de transporte y emisiones de CO₂, intuitivamente, podemos concluir que los modelos de localización de instalaciones que optimizan uno u otro objetivo pueden dar lugar a soluciones óptimas diferentes. Mientras que los modelos de minimización de costos encuentran ubicaciones óptimas más cercanas a los nodos de alta demanda, los modelos de minimización de CO₂ pueden considerar ubicaciones óptimas más cercanas a los nodos donde se requiere un mayor número de viajes para satisfacer la demanda del cliente.
Esta característica de los modelos de minimización de CO₂ puede observarse tanto en nodos de alta demanda como en nodos con restricciones de accesibilidad para camiones. Por lo tanto, en los problemas de localización de instalaciones, las soluciones obtenidas mediante la minimización de los costos de transporte no son necesariamente equivalentes a las soluciones obtenidas mediante la minimización de las emisiones de CO₂.
7.2. Modelos de Localización de Instalaciones Verdes
En esta sección, presentamos algunos modelos generales de localización de instalaciones que son comúnmente estudiados en la literatura de logística, incluyendo tanto modelos continuos como discretos. Posteriormente, discutimos algunas extensiones de estos modelos que incorporan las emisiones de CO₂ en las decisiones de localización.
7.2.1. Modelos Tradicionales de Localización de Instalaciones
El problema de localización de instalaciones tiene una historia extensa. Fue introducido por primera vez por Weber (1909), y en la literatura se pueden encontrar numerosas extensiones y aplicaciones. Para una explicación básica de los problemas de localización de instalaciones, nos referimos a Daskin (2008) y Daskin et al. (2005), y para revisiones más recientes, a Melo et al. (2009) y Revelle et al. (2008).
Típicamente, los problemas de localización de instalaciones se clasifican según su espacio de solución en continuos, si las instalaciones candidatas pueden ubicarse en cualquier punto dentro del área, o discretos, si las instalaciones candidatas están restringidas a un conjunto finito de ubicaciones (Daskin, 2008). Además, cuando los modelos continuos suponen que la demanda está distribuida de manera continua en una región de servicio, esta metodología es conocida como modelos analíticos de localización.
Las aproximaciones continuas y analíticas proporcionan una visión general de las ubicaciones óptimas y son comúnmente utilizadas por los investigadores para ofrecer directrices o generar conocimientos (Geofrion, 1976). En la literatura, se pueden encontrar diversas aplicaciones relacionadas con extensiones de modelos de localización, como el problema de localización de hubs (Saberi y Mahmassani, 2013), el diseño de redes de transporte de carga (Campbell, 2013) y el diseño de redes hub-and-spoke (Carlsson y Jia, 2013). Para los modelos analíticos, los métodos de solución se obtienen mediante análisis matemático, mientras que para los modelos continuos que no pueden resolverse analíticamente, se utilizan procedimientos numéricos iterativos que garantizan su convergencia hacia soluciones óptimas, como el algoritmo de Weiszfeld (1936) para el problema de Weber.
Para aplicaciones prácticas, las formulaciones discretas son más realistas, ya que proporcionan ubicaciones factibles y óptimas, aunque son más difíciles de resolver. En este tipo de modelos, las ubicaciones candidatas son preseleccionadas con base en información complementaria, como la proximidad a proveedores, disponibilidad de mano de obra, regulaciones locales y espacio físico disponible, entre otros factores.
El modelo básico que determina la ubicación óptima de instalaciones dentro de un conjunto finito de ubicaciones candidatas es conocido como el problema p-Median. El problema p-Median se define de la siguiente manera (ReVelle y Swain, 1970):
Sea el conjunto de nodos de demanda y el conjunto de ubicaciones candidatas.
Parámetros:
= demanda en el nodo
= distancia entre el sitio candidato de instalación y la ubicación del cliente
Variables de decisión:
= 1 si se ubica una instalación en el sitio , 0 en caso contrario
= fracción de la demanda en la ubicación del cliente que es atendida por la instalación en el sitio
El problema p-Median se formula de la siguiente manera (P1):
$$ \text{Min} \rightarrow \sum_{j \in J} \sum_{i \in I} h_i d_{ij} Y_{ij} $$
Sujeto a:
| $$ \sum_{j \in J} Y_{ij} = 1, \quad \forall i \in I $$ | (1) |
| $$ \sum_{j \in J} X_{j} = p $$ | (2) |
| $$ Y_{ij} - X_j \leq 0, \quad \forall i \in I, \forall j \in J $$ | (3) |
| $$ X_j \in \{0,1\}, \quad \forall j \in J $$ | (4) |
| $$ Y_{ij} \geq 0, \quad \forall i \in I, \forall j \in J $$ | (5) |
La función objetivo minimiza la distancia total ponderada por la demanda.
La restricción (1) establece que cada nodo de demanda es cubierto. La restricción (2) determina que se deben ubicar exactamente p instalaciones. La restricción (3) establece que una instalación solo puede estar activa si al menos un nodo de demanda está asignado a ella. Las restricciones (4) son las restricciones de integralidad. Las restricciones (5) son las restricciones de no negatividad.
Cuando se aplica a una red general, el problema p-Median puede ser difícil de resolver. Sin embargo, dado que la condición de asignación única se cumple en esta formulación (es decir, tomará naturalmente valores de 0 o 1), esta propiedad limita las ubicaciones potenciales de las instalaciones a los nodos de la red. Por lo tanto, esto reduce el número total de configuraciones posibles de ubicación a n! / (n−p)! p! donde es el número total de nodos de la red (Owen y Daskin, 1998). Sin embargo, una enumeración total de todas las soluciones posibles puede ser computacionalmente inviable. Kariv y Hakimi (1979) demostraron que el problema p-Median es NP-difícil (NP-hard).
El problema p-Median ha sido la base para diversas extensiones, como el problema de localización de instalaciones con costo fijo, tanto en su versión sin restricción de capacidad como en su versión con capacidad limitada, y en otros problemas como multi-ítem y multi-nivel (Geoffrion y Graves, 1974; Pirkul y Jayaraman, 1996). También tiene múltiples aplicaciones en el mundo real, tales como ubicación y asignación de plantas industriales (Daskin y Dean, 2005), diseño de redes de comunicación y transporte (Kalpakis et al., 2001; Ruffolo et al., 2007; Stephens et al., 1994), despliegue de sensores (Greco et al., 2010) y minería de datos (Christou, 2011). Otras aplicaciones se encuentran en ReVelle et al. (2008).
El problema p-Median también ha sido ampliamente estudiado en optimización combinatoria, y se han propuesto múltiples métodos de solución, tales como búsqueda en vecindario variable (Hansen y Mladenović, 1997), algoritmos genéticos (Hosage y Goodchild, 1986), búsqueda tabú (Rolland et al., 1997), búsqueda dispersa (García-López et al., 2003), optimización basada en colonia de hormigas (Kochetov et al., 2005) y simulated annealing (Murray y Church, 1996). Pullan (2008) presentó un algoritmo híbrido basado en población, que fue probado en diversas instancias de la literatura. Los resultados demostraron que el algoritmo encontró soluciones óptimas para muchos problemas, y, para otros, mejoró las mejores soluciones conocidas en la literatura.
Una extensión natural del problema p-Median es relajar el número de instalaciones a ubicar p e incluir un costo fijo de localización . Este problema se conoce como el problema de localización de instalaciones con costo fijo (P2) (Balinski, 1965):
$$ \text{Min} \rightarrow \sum_{j \in J} \sum_{i \in I} f_j X_j + \alpha \sum_{j \in J} \sum_{i \in I} h_i d_{ij} Y_{ij} $$
Sujeto a (1)–(5).
Cuando también se incluye la restricción (6) ∑i∈I hiYij − bjXj ≤ 0 , ∀j ∈ J, que limita la demanda asignada a la instalación a un máximo de bj, el modelo resultante (P3) se conoce como el problema de localización de instalaciones con capacidad. Similar al problema p-Median, el problema de localización de instalaciones con costo fijo también es NP-difícil. Los enfoques previos utilizados para resolver el problema p-Median pueden ser aplicables en este caso. Otros métodos heurísticos de solución incluyen la búsqueda tabú (Glover, 1989; Glover y Laguna, 1997) y el algoritmo dual ascendente (Erlenkotter, 1978), entre otros.
7.2.2. Emisiones de Carbono en Modelos de Localización de Instalaciones
Ahora discutimos algunos modelos que incluyen la estimación de emisiones de CO₂ en el problema de localización de instalaciones. Como se mencionó en la Sección 1, las emisiones de CO₂ del transporte en modelos de localización de instalaciones deben ser consideradas con cuidado, especialmente porque las estructuras de costos y emisiones de CO₂ no suelen ser equivalentes.
Sin embargo, algunos estudios demuestran que, incluso cuando se adopta la misma estructura de modelado, las soluciones obtenidas mediante la minimización de costos de transporte no siempre son equivalentes a las soluciones obtenidas mediante la minimización de emisiones de CO₂, especialmente en redes logísticas más complejas (por ejemplo, redes intermodales).
7.2.2.1. Modelos Analíticos y Continuos
Comenzamos analizando el estudio de Bouchery y Fransoo (2015) sobre el diseño de redes intermodales en el hinterland. Los autores presentan un modelo analítico cuyo objetivo es determinar la ubicación óptima de una instalación (en su ejemplo, una terminal de contenedores en el interior) considerando tres objetivos: costo, emisiones de carbono y cambio modal.
Se supone que la demanda es uniforme en una región rectangular, que representa el hinterland del puerto en cuestión. La densidad de la demanda es igual a p contenedores por kilómetro cuadrado, y el origen de los flujos (el puerto) se encuentra en las coordenadas (0,0).
El modelo supone que los costos de transporte y las emisiones de carbono tienen la misma estructura y considera dos opciones de transporte: envío directo (transporte en camión directamente desde el puerto hasta el cliente) y transporte intermodal (transporte en tren hasta una terminal intermodal y, posteriormente, transporte en camión desde la terminal hasta el cliente).
Los costos y emisiones de CO₂ al atender una zona de demanda de tamaño Ai mediante envío directo se expresan como Z0,iDS = δ0,i ρ Ai Z1 e E0,iDS = δ0,i ρ Ai E1, donde:
= distancia desde el puerto hasta el centro de gravedad de la zona de demanda (km)
= costo del transporte en camión por contenedor-kilómetro
= emisiones de carbono del transporte en camión (kg de CO₂ por contenedor-kilómetro)
Los costos y emisiones de CO₂ cuando se utiliza transporte intermodal se expresan como: Z0,jIT = δ0,T (ZF2 + ρ Ai Z2) + δT,i ρ Ai Z1 e E0,iIT = δ0,T (EF2 + ρ Ai E2) + δT,i ρ Ai E1, donde:
= distancia desde el puerto hasta la terminal intermodal en el interior (km)
= distancia desde la terminal hasta el centro de gravedad de la zona de demanda i (km)
= costo fijo del transporte ferroviario por km
= costo variable del transporte ferroviario por contenedor-kilómetro
= emisiones fijas asociadas al transporte ferroviario (kg de CO₂ por km)
= emisiones lineales del transporte ferroviario (kg de CO₂ por contenedor-kilómetro)
Los autores identifican soluciones óptimas basadas en datos europeos. Sus resultados muestran que la terminal intermodal está ubicada más cerca del puerto cuando la optimización se basa en costos y más lejos del puerto cuando la optimización se basa en emisiones de carbono. Este resultado demuestra que, incluso cuando los costos y las emisiones de CO₂ tienen la misma estructura, existen diferencias significativas en las soluciones óptimas para ambas formulaciones.
Este efecto se explica por las diferencias en los parámetros fijos del transporte ferroviario, lo que también es consistente con el hecho de que el transporte ferroviario con alta utilización es más eficiente en términos de emisiones que el transporte por carretera, pero es más costoso en términos de costos. Para más detalles, nos remitimos al estudio completo (Bouchery y Fransoo, 2015).
Aunque se pueden encontrar algunos otros artículos sobre modelos continuos de localización de instalaciones verdes en la literatura, el área sigue siendo limitada. Buyuksaatci y Esnaf (2014) presentan un problema de localización de instalaciones basado en emisiones de carbono, considerando la minimización de las emisiones de CO₂ utilizando el método del centro de gravedad. El estudio emplea una formulación basada en el GHG Protocol, pero no analiza ningún impacto gerencial ni implicaciones derivadas de la formulación propuesta.
7.2.2.2. Modelos Discretos
Ahora discutimos los estudios sobre modelos de localización de instalaciones verdes con formulaciones discretas. Diabat y Simchi-Levi (2010) presentan un problema de localización de instalaciones de múltiples niveles y múltiples productos con una restricción de carbono. Su problema consiste en decidir la ubicación óptima de plantas y centros de distribución y la asignación de flujos, de manera que se minimicen los costos totales sin que las emisiones de carbono superen un límite específico. El modelo estima las emisiones de carbono en la distribución utilizando un factor de emisión por distancia (toneladas de CO₂ por km), por lo que no considera el impacto de la carga en las emisiones de CO₂ (ver Capítulo 5 de Blanco y Sheffi, 2024). A pesar de esta suposición simplificada, la conclusión general es intuitiva: si la restricción de emisiones de carbono se vuelve más estricta, los costos de la cadena de suministro aumentan.
Elhedhli y Merrick (2012) estudian un problema de diseño de redes de cadena de suministro que considera las emisiones de CO₂. El objetivo del estudio es minimizar simultáneamente los costos logísticos y los costos ambientales de las emisiones de CO₂, determinando estratégicamente la ubicación de los almacenes dentro de la red de distribución. El modelo considera la estimación de emisiones de CO₂ del GHG Protocol y emplea un parámetro de conversión para transformar las emisiones de CO₂ en costos. Esta metodología permite incluir el costo de las emisiones de carbono en el diseño de la cadena de suministro. Los resultados experimentales demuestran que la inclusión de costos de carbono conduce a soluciones en las que se abren más centros de distribución, reduciendo así las emisiones de CO₂ en el transporte.
Aunque el estudio proporciona perspectivas gerenciales interesantes, el modelo utiliza métodos agregados para estimar las emisiones de CO₂ del transporte, como el GHG Protocol con factores de emisión de la EPA. Velázquez-Martínez et al. (2014a) analizan los efectos del uso de diferentes niveles de agregación en la medición de las emisiones de carbono del transporte, y demuestran que los errores asociados con la agregación pueden ser significativos y sistemáticos. Esto sugiere que incrementar el nivel de detalle en el problema de localización de instalaciones es necesario.
El costo no siempre es el único factor que impulsa la reducción de las emisiones de CO₂ en el transporte. Por ejemplo, las empresas pueden estar sujetas a un sistema de cap-and-trade o pueden utilizar la reducción de emisiones de carbono como un factor estratégico de gestión de marca, diferenciación de productos o motivación de empleados (CDP, 2011a, b). Esto sugiere que una formulación práctica de modelos de localización verde debería considerar simultáneamente los objetivos de costo y emisiones de CO₂.
Una posible alternativa para considerar ambos objetivos (costo y emisiones de CO₂) es modelar el problema de localización de instalaciones verdes en un contexto multiobjetivo. La mayoría de los problemas del mundo real involucran naturalmente múltiples objetivos (minimizar costos, maximizar el nivel de servicio, minimizar las emisiones de CO₂, etc.).
La optimización multiobjetivo permite definir un conjunto de soluciones eficientes (o frontera de Pareto), donde no existe otra solución que las domine, es decir, cada solución en el conjunto es estrictamente mejor que las demás en al menos un objetivo y no es peor en los otros objetivos (Coello, 2009). Estas soluciones eficientes suelen ser preferidas en lugar de soluciones únicas, ya que son más aplicables en problemas reales, en los que la decisión final siempre implica un trade-off (Konak et al., 2006).
Siguiendo esta línea de investigación, Harris et al. (2014) presentan una formulación del problema de localización de instalaciones con costo fijo (P3) con dos funciones objetivo: costos y emisiones de CO₂. El modelo de localización de instalaciones considera depósitos individuales con capacidades , donde cada cliente es atendido directamente por un solo depósito, asegurando que se respete la condición de fuente única en el modelo. Esto permite construir un algoritmo de solución que primero determina qué instalaciones abrir y luego asigna los clientes a las instalaciones abiertas. El estudio propone una expresión para estimar las emisiones de CO₂ del transporte basada en el GHG Protocol, es decir, las emisiones de CO₂ del transporte son linealmente dependientes de la distancia recorrida y la demanda.
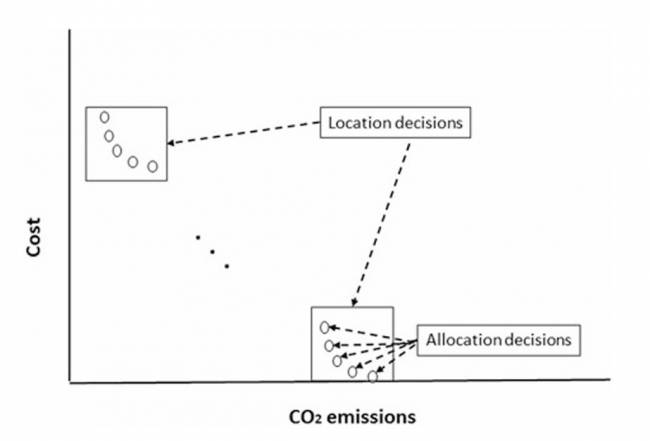
El estudio analiza un método de optimización multiobjetivo para el modelo de localización de instalaciones con costos y CO₂, en el cual el tomador de decisiones puede explorar soluciones de trade-off para la asignación de clientes en función de la ubicación preseleccionada de las instalaciones. La Figura 7.2 (Harris et al., 2014) presenta diferentes soluciones para la decisión de localización y, para cada decisión, la posible asignación de clientes.
El artículo se enfoca en los métodos de solución y proporciona un marco de análisis para evaluar los trade-offs entre costo y emisiones de CO₂ en modelos de localización de instalaciones.
Dado que observamos que todos los estudios previos concluyen que un mayor número de instalaciones abiertas implica una reducción en las emisiones de CO₂ del transporte (y, generalmente, más instalaciones también implican costos más altos), podemos argumentar que una forma práctica de analizar el trade-off entre costo y emisiones de CO₂ en la localización de instalaciones es simplificar la formulación al no incluir la emisión fija por instalación abierta. Por lo tanto, nos interesa estudiar el efecto del costo del transporte versus las emisiones de CO₂ del transporte manteniendo una cantidad fija de instalaciones previamente definidas (es decir, utilizando el problema p-Median).
Velázquez-Martínez et al. (2014b) estudian el trade-off entre costos y emisiones de CO₂ mediante un enfoque multiobjetivo para el problema de localización de instalaciones. El modelo corresponde al problema p-Median, considerando funciones objetivo tanto para el costo como para las emisiones de CO₂. Las suposiciones generales del problema p-Median se aplican a este modelo, es decir, la demanda es determinística y las ubicaciones candidatas son conocidas de antemano. Además, el modelo también supone que la empresa puede gestionar múltiples camiones con diferentes capacidades, y que estos camiones son asignados según las restricciones de los nodos de demanda (o según la política de la empresa). Estas suposiciones permiten que el modelo incluya la posibilidad de que ciertos clientes solo puedan ser atendidos por ciertos tipos de camiones, cada uno con estructuras de costos diferentes.
Para formular la función objetivo de emisiones de carbono, los autores incorporan la metodología NTM en la función objetivo (Velázquez-Martínez et al., 2014b).
Nótese que representa el número de viajes necesarios para atender al cliente y, por lo tanto, afecta la distancia total recorrida:
$$ l \sum_{j \in J} \sum_{i \in I} d_{ij} \left[ f_i^e \left\lfloor \frac{h_i}{W_i} \right\rfloor + \left( f_i^f - f_i^e \right) \frac{h_i}{W_i} \right] Y_{ij} $$
Esta formulación permite comprender en mayor detalle el trade-off entre distancia () y utilización () al tomar decisiones de localización y asignación de instalaciones. Por ejemplo, cuando se atiende a los clientes con una flota homogénea (es decir, para todo ), las soluciones de localización son las mismas que las obtenidas por P1, es decir, las instalaciones se ubican más cerca de los clientes con mayor demanda, lo que implica que minimizar el costo del transporte es equivalente a minimizar las emisiones de CO₂. Sin embargo, cuando se atiende a los clientes con una flota no homogénea (por ejemplo, debido a restricciones de camiones impuestas por regulaciones o infraestructura de transporte), las instalaciones pueden ubicarse más cerca de los clientes atendidos por camiones pequeños. Esto puede explicarse por el hecho de que estos clientes requieren múltiples viajes, lo que implica que se recorre una mayor distancia para atenderlos, incrementando así las emisiones de CO₂.
7.3. Implicaciones Prácticas de los Modelos de Localización Verde
El transporte es uno de los principales factores contribuyentes a las emisiones globales de carbono y, por lo tanto, en el contexto de modelos de localización de instalaciones en la distribución, las emisiones del transporte pueden ser sustancialmente más altas que las emisiones derivadas de la producción o el almacenamiento. Además, dado que los modelos de localización de instalaciones definen la configuración de las entregas, los modelos de localización verde se convierten en una alternativa importante para reducir las emisiones de CO₂ en la logística. Como el transporte suele incluirse en el Alcance 3 del inventario de Gases de Efecto Invernadero (GHG) y generalmente representa la mayor fuente de emisiones en una cadena de suministro, las empresas pueden empezar a centrarse más en aumentar el número de centros de distribución para mejorar el alcance a los clientes. Hemos observado este fenómeno en los principales minoristas, como Amazon, como resultado de su modelo de negocios basado en envíos rápidos y la necesidad de aumentar la velocidad del servicio al cliente (Dastin, 2020).
Mientras que las soluciones de minimización de costos tienden a ubicar las instalaciones más cerca de los clientes con alta demanda, las soluciones de minimización de emisiones de CO₂ tienden a ubicar las instalaciones más cerca de clientes con restricciones de accesibilidad para camiones. Esto se debe a que las restricciones para camiones determinan el número de viajes necesarios para atender a los clientes, y este factor tiene un impacto mayor que el crecimiento de la demanda y/o la utilización de vehículos.
Este aspecto puede ser particularmente relevante para empresas que gestionan flotas de vehículos no homogéneas o para responsables de políticas en áreas urbanas densamente pobladas, donde la demanda es alta (debido a la alta densidad de habitantes y la existencia de pequeñas tiendas), pero los vehículos pesados no están permitidos. Se pueden necesitar nuevas regulaciones para equilibrar la accesibilidad de los camiones grandes en ciertos períodos, con el fin de mejorar la eficiencia logística y reducir el número de vehículos pequeños en esas zonas.
En algunos problemas logísticos, incluso cuando se utilizan enfoques agregados para estimar las emisiones de CO₂ del transporte, lo que hace que la formulación comparta la misma estructura que el costo de transporte, las soluciones de localización pueden ser sustancialmente diferentes. Para empresas interesadas en aumentar el cambio modal o en utilizar más transporte intermodal, estas estrategias pueden provocar un aumento en las emisiones de CO₂. En particular, cuando se utilizan modos de transporte diferentes, como en redes intermodales, la diferencia en los parámetros de costo de transporte y emisiones de CO₂ puede conducir a un conjunto completamente distinto de soluciones para ambas funciones objetivo.
Un modelo multiobjetivo para la localización de instalaciones verdes puede proporcionar a los tomadores de decisiones un marco de análisis para evaluar el trade-off entre costo y emisiones de CO₂. Este enfoque puede aportar una nueva herramienta para que las empresas definan mejores estrategias para reducir las emisiones de CO₂. Dado que los tomadores de decisiones probablemente buscan alternativas que reduzcan las emisiones sin aumentar excesivamente los costos, la modelización multiobjetivo proporciona un conjunto de soluciones de trade-off que antes no eran evidentes en modelos con un solo objetivo.
Esto puede implicar que surjan nuevas soluciones con una compensación adecuada entre costo y emisiones de CO₂. Por ejemplo, ubicaciones con pequeños aumentos en costos pueden generar reducciones significativas en las emisiones de CO₂.
7.4. Direcciones para Trabajos Futuros
El área de localización de instalaciones verdes sigue siendo poco explorada en la investigación. Dado que los costos de transporte y las emisiones de CO₂ no tienen la misma estructura, se debe considerar una formulación específica para los modelos de minimización de emisiones de CO₂ en la localización de instalaciones. Desafortunadamente, pocos estudios consideran expresiones detalladas para estimar las emisiones de CO₂ del transporte en modelos de localización, y la mayoría de ellos utiliza el GHG Protocol y el GLEC Framework; por lo tanto, el efecto completo de estas emisiones aún no ha sido completamente estudiado ni comprendido.
Además, pocas empresas han implementado estrategias que utilicen la localización de instalaciones como una herramienta para reducir su impacto ambiental. Por ello, se necesitan más aplicaciones de estos modelos en casos prácticos, de modo que se puedan validar en la práctica y comprender mejor los trade-offs que implican.
Asimismo, pocos artículos en la literatura incluyen en sus formulaciones las emisiones generadas por las propias instalaciones, y generalmente solo consideran las emisiones derivadas de la producción de electricidad. La mayoría de los modelos se centran en las emisiones causadas por el transporte, específicamente en la distribución de última milla. Sin embargo, no se ha investigado el impacto del transporte de materias primas en la localización de instalaciones, lo que sugiere la necesidad de desarrollar nuevas formulaciones de modelos que aborden esta brecha en la investigación.
En este capítulo, hemos limitado nuestra discusión al impacto de las emisiones de carbono provenientes de fuentes móviles. Sin embargo, considerar diferentes fuentes de energía para las instalaciones (energía eólica, combustibles, etc.) e incluirlas en futuros modelos de localización de instalaciones verdes para analizar el impacto de las fuentes de energía en las ubicaciones planificadas representa una prometedora línea de investigación, especialmente en relación con la estrategia de electrificación del sector del transporte.
Las instalaciones pueden desempeñar un papel clave en el apoyo a la electrificación del transporte, funcionando como puntos de almacenamiento de baterías eléctricas u otras fuentes de energía, así como hubs energéticos para permitir carga conectada y estaciones de recarga.
Referencias
Akçelik R, Besley M (2003) Operating cost, fuel consumption, and emission models in aaSIDRA and aaMOTION. In: 25th Conference of Australian Institutes of Transport Research (CAITR 2003). University of South Australia, Adelaide, Australia
Balinski ML (1965) Integer programming: methods, uses, computation. Manag Sci 12:253–313 Blanco EE, Sheffi Y (2024) Green logistics. In: Bouchery Y, Corbett CJ, Fransoo JC (eds)
Sustainable supply chains: a research-based textbook on operations and strategy. Springer, Cham
Bouchery Y, Fransoo JC (2015) Cost, carbon emissions and modal shift in intermodal network design decisions. Int J Prod Econ 164:388–399
Boukherroub T, Bouchery Y, Tan T, Fransoo J, Corbett C (2024) Carbon footprinting in supply chains: measurement, reporting and disclosure. In: Bouchery Y, Corbett CJ, Fransoo JC (eds) Sustainable supply chains: a research-based textbook on operations and strategy. Springer, Cham
Buyuksaatci S, Esnaf S (2014) Carbon emission based optimization approach for the facility location problem. Online J Sci Technol 4(1)
Campbell JF (2013) A continuous approximation model for time definite many-to-many transportation. Transp Res B Methodol 54:100–112
Carlsson JG, Jia F (2013) Euclidean hub-and-spoke networks. Oper Res 61:1360–1382 CDP (2011a) Carbon disclosure project. Available on www.cdproject.net/.
CDP (2011b) Carbon disclosure project. Supply chain report: ATKearney. Available at https://www.cdproject.net/CDPResults/CDP-2011-Supply-Chain-Report.pdf.
Cholette S, Venkat K (2009) The energy and carbon intensity of wine distribution: a study of logistical options for delivering wine to consumers. J Clean Prod 17(16):1401–1413
Christou IT (2011) Coordination of cluster ensembles via exact methods. IEEE Trans Pattern Anal Machine Intell 2:279–293
Coello CA (2009) Evolutionary multi-objective optimization: some current research trends and topics that remain to be explored. Front Comput Sci China 3(1):18–30
Daskin MS (2008) What you should know about location modeling. Wiley Periodicals
Daskin MS, Dean L (2005) Location of health care facilities. Oper Res Health Care J 70:43–76


















