Projeto de Rede Verde e Localização de Instalações
- localização verde
- modelos de localização
- emissões de carbono
- otimização logística
- custos de transporte
- transporte intermodal
- logística sustentável
- supply-chain
7.1. Introdução
As emissões do transporte representam uma parcela significativa das emissões globais, sendo que o transporte de carga é responsável por uma parte considerável dessas emissões. A redução das emissões do transporte pode ser alcançada por meio de diferentes escolhas logísticas, como a mudança do modo de transporte, a alteração das rotas ou a modificação do carregamento dos veículos na rede (ver Capítulo 5 de Blanco e Sheffi (2024) para mais detalhes sobre logística verde). Essas escolhas logísticas são fortemente influenciadas pelas políticas de estoque adotadas por uma empresa (ver Capítulo 6 de Marklund e Berling (2024) para mais informações sobre gestão de estoques sustentáveis). Por exemplo, permitir um modo de transporte mais sustentável, porém mais lento, normalmente exige um aumento ou um reposicionamento dos estoques na rede de suprimentos.
Além das escolhas logísticas e das políticas de estoque, o desempenho do transporte em termos de custos e emissões é fortemente determinado pelo desenho da rede. Nos sistemas de distribuição, isso se refere, em particular, à localização dos centros de distribuição ou de outros hubs logísticos, como fábricas ou terminais cross-docking. Neste capítulo, abordamos a questão da localização desses hubs de transporte.
O problema logístico que define a configuração da entrega de bens de uma empresa é conhecido como problema de localização de instalações. Esse problema consiste em determinar a localização de um conjunto de instalações (por exemplo, fábricas, terminais cross-docking, centros de distribuição) dentro de um espaço físico, de modo que toda a demanda dos clientes seja atendida por pelo menos uma instalação e que o custo total de transporte seja minimizado. Embora a literatura sobre localização de instalações seja extensa e bem estabelecida, neste capítulo focamos em uma variante desse problema que inclui explicitamente as emissões de carbono do transporte na formulação. Chamamos esse problema de localização de instalações verdes, pois seu objetivo é minimizar as emissões de CO₂ no transporte.
Ao limitar nosso escopo às emissões de fontes móveis (ou seja, provenientes do transporte), não consideramos as emissões de fontes estacionárias que poderiam ser influenciadas pela decisão de localização. Sem esgotar todas as possibilidades, alguns exemplos dessas emissões incluem:
-
Emissões nos centros de distribuição: relacionadas ao consumo de energia das instalações, que geralmente incluem eletricidade para iluminação, automação e refrigeração. Em alguns casos, podem existir economias de escala associadas ao desenho da rede. Dados do setor sugerem que, na maioria das redes de distribuição, as emissões dos centros de distribuição representam menos de 10% do total das emissões logísticas.
-
Disponibilidade de fontes de energia locais: para operações intensivas em energia, a presença de fontes de energia renovável pode ter um impacto significativo na redução das emissões da cadeia de suprimentos. Por exemplo, a localização de uma usina de alumínio em uma região com disponibilidade de eletricidade geotérmica poderia reduzir as emissões totais da cadeia de suprimentos, mesmo que as emissões do transporte aumentassem.
A exclusão das emissões de fontes estacionárias nos modelos discutidos neste capítulo implica que estamos nos restringindo, na prática, às redes de distribuição e às decisões de localização de centros de distribuição e terminais cross-docking. No entanto, em nossa discussão, utilizamos o termo mais geral "instalação".
Normalmente, ao projetar seus canais de distribuição, as empresas selecionam os locais de armazéns e centros de distribuição com o objetivo de atender à demanda dos clientes minimizando a distância percorrida (ou os custos de transporte). Neste capítulo, revisamos alguns modelos que incorporam as emissões de CO₂ do transporte no problema de localização de instalações sem restrição de capacidade. Em seguida, discutimos as soluções obtidas quando o número de instalações a serem localizadas é fixado, utilizando o problema p-Mediana. Apresentamos ainda discussões e implicações gerenciais para a localização de instalações verdes. Nosso objetivo é entender se as decisões de localização baseadas na minimização de custos são diferentes daquelas obtidas pelo modelo de localização de instalações verdes.
7.1.1. Localização de Instalações e Emissões de Carbono
As decisões de localização de instalações são, em geral, tomadas com base nos custos associados, que incluem o transporte (das instalações até os clientes) e a operação da instalação (produção e armazenamento). Como discutido anteriormente, podemos dividir as principais fontes de emissões de CO₂ associadas à localização de instalações de maneira semelhante: emissões de fontes móveis (transporte) e emissões de fontes estacionárias (produção, armazenamento e manuseio). Um maior número de instalações reduz as emissões de CO₂ provenientes de fontes móveis, pois diminui a distância entre a instalação e os clientes. No entanto, isso aumenta as emissões de fontes estacionárias devido à maior quantidade de instalações operando simultaneamente. Assim, o desafio na localização de instalações verdes é definir o número e a posição adequados das instalações para atender um conjunto de clientes minimizando as emissões globais de CO₂.
Diversos estudos mostram que transporte e produção contribuem significativamente para as emissões de CO₂. Por exemplo, os três principais setores responsáveis pelas emissões nos países desenvolvidos são geração de eletricidade, manufatura intensiva em energia e transporte (Agência Europeia do Meio Ambiente, 2018). Enquanto a geração de eletricidade e a manufatura intensiva em energia são consideradas dentro dos Escopos 1 e 2 do inventário de GEE (Gases de Efeito Estufa), as emissões de transporte por prestadores de serviço são classificadas dentro do Escopo 3 (ver Capítulo 3 de Boukherroub et al. (2024) para mais detalhes). As emissões do Escopo 3 frequentemente representam a maior fonte de emissões de GEE, podendo corresponder a mais de 90% da pegada de carbono de uma empresa (World Business Council for Sustainable Development, 2021).
Além disso, quando o problema de localização de instalações envolve centros de distribuição em vez de plantas industriais, as emissões de CO₂ provenientes de fontes móveis são significativamente maiores do que as de fontes estacionárias, já que, nesse caso, as emissões estacionárias se restringem às atividades dos centros de distribuição. Estudos indicam que as emissões de armazenamento e manuseio são substancialmente menores do que as emissões do transporte, podendo ser até 10 vezes inferiores para certos produtos (Cholette e Venkat, 2009). Portanto, neste capítulo, concentramos nossa análise na localização de centros de distribuição, com foco principal nas emissões de carbono provenientes do transporte.
Existem diversas práticas implementadas na indústria para reduzir emissões de carbono, tornando as operações logísticas mais eficientes e sustentáveis (por exemplo, Heineken Sustainability Report, 2013; Groupe Danone, 2014; MIT-EDF, 2013). No entanto, poucas empresas consideraram a localização de centros de distribuição como uma alternativa estratégica para reduzir as emissões de CO₂ no transporte. Um exemplo é a Unilever, que aumentou o número de hubs regionais e posicionou essas instalações mais próximas dos clientes (Unilever Press Release, 2013).
A localização de instalações é um fator crítico para a eficiência e a eficácia operacional da cadeia de suprimentos. Instalações mal posicionadas podem gerar custos excessivos e reduzir o nível de serviço, independentemente da otimização de decisões táticas, como roteirização de veículos e gestão de estoques (Daskin et al., 2005). Neste capítulo, demonstramos que a escolha da localização das instalações pode impactar significativamente as emissões de CO₂ provenientes do transporte na cadeia de suprimentos. Note-se que os principais fatores determinantes das emissões de carbono no transporte incluem distância percorrida, carga do veículo (Greenhouse Gas Protocol Standard, 2015; Smart Freight Centre, 2016) e número de viagens necessárias para atender à demanda dos clientes (Network for Transport Measures, 2022). A alteração do número e da localização das instalações na rede de distribuição impacta diretamente todos esses fatores, influenciando a pegada de carbono do transporte.
7.1.2. Trade-off Entre Custo e Emissões de Carbono na Localização de Instalações
Os custos de transporte () em problemas de localização de instalações normalmente levam em consideração a demanda () e a distância (). Esses custos são geralmente modelados como uma função objetivo utilizando a distância total ponderada pela demanda (), assumindo um custo constante por unidade de distância e por unidade transportada (Revelle et al., 2008). Observe que essa formulação encontra soluções ótimas em que as instalações estão mais próximas das regiões com alta demanda. No entanto, para minimizar as emissões de CO₂ do transporte, soluções eficazes podem exigir uma análise diferente.
As emissões de CO₂ do transporte são afetadas por uma variedade de condições relacionadas ao tipo de veículo (por exemplo, potência do motor, torque, tipo de combustível, coeficiente de arrasto aerodinâmico) e às características da operação de entrega (por exemplo, tipo de estrada, inclinação, velocidade do veículo, carga) (Akçelik e Besley, 2003). Devido à falta de informações detalhadas sobre a operação de entrega (inclinações específicas, velocidade, aerodinâmica, etc.) durante o processo de tomada de decisão, as empresas normalmente utilizam métodos mais agregados baseados em atividade para estimar as emissões de CO₂ (ver Capítulo 3 de Boukherroub et al. (2024) para mais informações sobre pegada de carbono). Alguns dos métodos baseados em atividade mais comuns são o GHG Protocol, o Global Logistics Emissions Council (GLEC) Framework (Greene e Lewis, 2016) e a metodologia desenvolvida pela Network for Transport Measures (NTM).
Observamos que um modelo de localização de instalações baseado no GHG Protocol ou nas metodologias GLEC forneceria localizações ótimas idênticas às soluções do modelo de minimização de custos, ou seja, as localizações ótimas tenderiam a estar mais próximas das regiões com alta demanda. Isso ocorre porque esses modelos de estimativa multiplicam a distância e a carga por um fator de intensidade de carbono que assume a utilização dos veículos, ou seja, não considera explicitamente o número de viagens necessárias para entregar a carga específica. No entanto, isso nem sempre ocorre quando se emprega uma metodologia como a NTM.
A metodologia NTM requer parâmetros mais detalhados: eficiência do consumo de combustível, distância percorrida e peso por remessa (NTM Road, 2010). A eficiência do consumo de combustível é uma função do tipo de caminhão, do fator de carga e do tipo de estrada. O NTM utiliza a base de dados da European Assessment and Reliability of Transport Emission Models and Inventory Systems, que desenvolveu um modelo detalhado de emissões para todos os modais de transporte, a fim de fornecer estimativas de emissões consistentes em níveis nacional, internacional e regional (TRL, 2010). O modelo de estimativa NTM é
$$ E = l \left[ d \left( f^e + \left( f^f - f^e \right) \frac{w}{W} \right) \right] , $$
onde
E = emissões totais em gramas de CO₂
l = fator de emissão constante (2621 gramas de CO₂/litro)
fe = consumo de combustível do veículo vazio (litros/km)
ff = consumo de combustível do veículo totalmente carregado (litros/km)
W = capacidade do caminhão
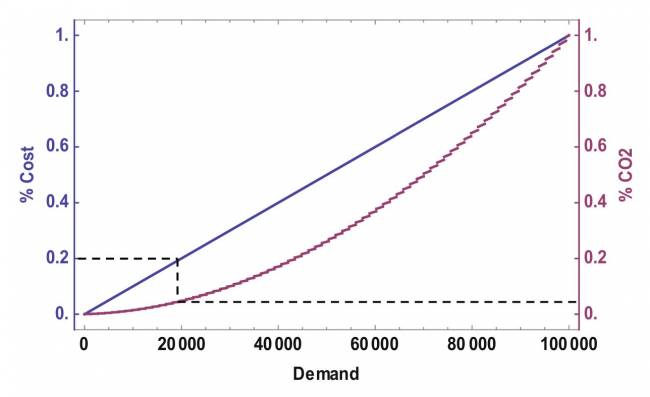
Comparando o custo de transporte e as emissões de CO₂, observe que o efeito da distância é linear em ambas as expressões. No entanto, a demanda e a capacidade do caminhão afetam os custos de transporte de maneira diferente das emissões de CO₂. A Figura 7.1 apresenta a comparação entre os custos de transporte e as emissões de CO₂ para diferentes níveis de demanda. Neste exemplo, utilizamos um caminhão de 14 toneladas para vias urbanas, considerando que 100 unidades de demanda equivalem a 1 tonelada.
Note que o aumento da demanda não se traduz em um crescimento linear das emissões de CO₂, como ocorre com os custos. Por exemplo, uma demanda de 20.000 unidades pode aumentar os custos em até 20%, enquanto o aumento nas emissões de CO₂ é de aproximadamente 5%. O gráfico também mostra que um aumento na demanda impacta as emissões de CO₂ principalmente quando esse crescimento implica um maior número de viagens.
Devido a essas diferenças nas estruturas de custo de transporte e emissões de CO₂, intuitivamente, podemos concluir que modelos de localização de instalações que utilizam uma ou outra função objetivo podem resultar em soluções ótimas diferentes. Enquanto modelos de minimização de custo encontram localizações ótimas mais próximas de nós de alta demanda, modelos de minimização de CO₂ podem também considerar localizações mais próximas de nós onde um maior número de viagens seja necessário para atender à demanda do cliente.
Essa característica dos modelos de minimização de CO₂ pode ser observada tanto em nós de alta demanda quanto em nós com restrições de acessibilidade para caminhões. Portanto, em problemas de localização de instalações, as soluções obtidas pela minimização dos custos de transporte não são necessariamente equivalentes às soluções obtidas pela minimização das emissões de CO₂ no transporte.
7.2. Modelos de Localização de Instalações Verdes
Nesta seção, apresentamos alguns modelos gerais de localização de instalações que são amplamente estudados na literatura de logística, incluindo modelos contínuos e discretos. Posteriormente, discutimos algumas extensões desses modelos que estudam as emissões de CO₂ nas decisões de localização.
7.2.1. Modelos Tradicionais de Localização de Instalações
O problema de localização de instalações tem uma longa história. Foi introduzido pela primeira vez por Weber (1909), e um grande número de extensões e aplicações pode ser encontrado na literatura. Para uma explicação básica dos problemas de localização de instalações, referimo-nos a Daskin (2008) e Daskin et al. (2005), e para revisões mais recentes, referimo-nos a Melo et al. (2009) e Revelle et al. (2008).
Tipicamente, os problemas de localização de instalações são classificados com base em seu espaço de solução como contínuos, caso as localizações candidatas possam ser situadas em qualquer ponto dentro da área, ou discretos, caso as instalações candidatas sejam restritas a um conjunto finito de locais possíveis (Daskin, 2008). Além disso, quando modelos contínuos assumem que as demandas estão distribuídas continuamente ao longo de uma região de serviço, essa abordagem é conhecida como modelos analíticos de localização.
As abordagens contínuas e analíticas fornecem uma visão geral das localizações ótimas e são comumente utilizadas por pesquisadores para fornecer diretrizes ou insights (Geofrion, 1976). Uma variedade de aplicações pode ser encontrada na literatura relacionada a extensões de modelos de localização, tais como o problema de localização de hubs (Saberi e Mahmassani, 2013), redes de transporte de carga (Campbell, 2013) e projeto de redes hub-and-spoke (Carlsson e Jia, 2013). Para modelos analíticos, os métodos de solução são derivados por meio de análise matemática, enquanto para modelos contínuos que não podem ser resolvidos analiticamente, procedimentos numéricos iterativos garantem sua convergência para soluções ótimas, por exemplo, o algoritmo de Weiszfeld (1936) para o problema de Weber.
Para aplicações práticas, formulações discretas são mais realistas para fornecer localizações viáveis e ótimas, mas são mais difíceis de resolver. Para esse tipo de modelo, locais candidatos são pré-selecionados com base em informações complementares, tais como proximidade de fornecedores, proximidade da mão de obra, regulamentações locais e espaço físico disponível, entre outros. O modelo básico que localiza a instalação ótima entre um conjunto de locais candidatos em um espaço discreto é conhecido como o problema p-Mediana. O problema p-Mediana é definido da seguinte forma (ReVelle e Swain, 1970):
Seja um conjunto de nós de demanda e um conjunto de locais candidatos.
Parâmetros:
= demanda no nó
= distância entre o local candidato da instalação e a localização do cliente
Variáveis de decisão:
= 1 se localizarmos uma instalação no local , 0 caso contrário
= fração da demanda no local do cliente que é atendida pela instalação no local
O problema p-Mediana é então formulado da seguinte forma (P1):
$$ \text{Min} \rightarrow \sum_{j \in J} \sum_{i \in I} h_i d_{ij} Y_{ij} $$
Sujeito a:
| $$ \sum_{j \in J} Y_{ij} = 1, \quad \forall i \in I $$ | (1) |
| $$ \sum_{j \in J} X_{j} = p $$ | (2) |
| $$ Y_{ij} - X_j \leq 0, \quad \forall i \in I, \forall j \in J $$ | (3) |
| $$ X_j \in \{0,1\}, \quad \forall j \in J $$ | (4) |
| $$ Y_{ij} \geq 0, \quad \forall i \in I, \forall j \in J $$ | (5) |
A função objetivo minimiza a distância total ponderada pela demanda. Restrição (1) estabelece que cada nó de demanda é atendido. Restrição (2) define que p instalações são localizadas. Restrição (3) estabelece que a instalação é aberta quando um nó de demanda é alocado. Restrições (4) são as restrições de integralidade. Restrições (5) são as restrições de não negatividade.
Quando aplicado a uma rede geral, o problema p-Mediana pode ser difícil de resolver. No entanto, como a condição de fonte única é válida nesta formulação (ou seja, naturalmente assumirá valores de zero ou um), essa propriedade limita os locais potenciais das instalações aos nós da rede e, portanto, reduz o número de configurações possíveis de localização para n! /(n−p)! p! onde é o número de nós (Owen e Daskin, 1998). No entanto, uma enumeração total de todas as soluções possíveis pode ser computacionalmente inviável. Kariv e Hakimi (1979) demonstraram que o problema p-Mediana é NP-difícil.
O problema p-Mediana tem sido a base de múltiplas extensões, tais como o problema de localização de instalações com custo fixo, tanto na versão sem capacidade quanto com capacidade, e em outros problemas como multi-itens e multi-estágios (Geoffrion e Graves, 1974; Pirkul e Jayaraman, 1996). Também possui múltiplas aplicações no mundo real, como alocação de instalações industriais (Daskin e Dean, 2005), projeto de redes (Kalpakis et al., 2001; Ruffolo et al., 2007; Stephens et al., 1994), desdobramento de sensores (Greco et al., 2010), e mineração de dados (Christou, 2011). Outras aplicações são apresentadas em ReVelle et al. (2008).
O problema p-Mediana também tem atraído grande atenção na otimização combinatória, e muitos métodos de solução foram propostos para resolvê-lo. Por exemplo, busca em vizinhança variável (Hansen e Mladenović, 1997), algoritmo genético (Hosage e Goodchild, 1986), busca tabu (Rolland et al., 1997), busca dispersa (García-López et al., 2003), otimização baseada em colônia de formigas (Kochetov et al., 2005), e simulated annealing (Murray e Church, 1996). Pullan (2008) apresenta um algoritmo híbrido baseado em população que foi testado em diversas instâncias da literatura. Os resultados mostram que o algoritmo encontra soluções ótimas para muitos problemas e, para outros, foi capaz de melhorar as melhores soluções conhecidas na literatura.
Uma extensão natural do problema p-Mediana é relaxar o número de instalações a serem abertas e incluir um custo fixo de localização fj. Esse problema é chamado de problema de localização de instalações com custo fixo (P2) (Balinski, 1965):
$$ \text{Min} \rightarrow \sum_{j \in J} \sum_{i \in I} f_j X_j + \alpha \sum_{j \in J} \sum_{i \in I} h_i d_{ij} Y_{ij} $$
Sujeito a (1)–(5).
Quando também incluímos a restrição (6) ∑i∈I hiYij − bjXj ≤ 0 , ∀j ∈ J, que limita a demanda atribuída à instalação j ∈ J a um máximo de bj, o modelo resultante (P3) é conhecido como problema de localização de instalações com capacidade. Assim como o problema p-Mediana, o problema de localização de instalações com custo fixo também é NP-difícil. Métodos anteriores usados para resolver o problema p-Mediana também podem ser aplicáveis nesse caso. Outros métodos heurísticos de solução incluem busca tabu (Glover, 1989; Glover e Laguna, 1997) e o algoritmo dual ascendente (Erlenkotter, 1978), entre outros.
7.2.2. Emissões de Carbono em Modelos de Localização de Instalações
Agora discutimos alguns modelos que incluem a estimativa de emissões de CO₂ no problema de localização de instalações. Como mencionado na Seção 1, as emissões de CO₂ do transporte devem ser consideradas com cautela, especialmente porque custos e emissões de CO₂ não compartilham, necessariamente, a mesma estrutura. No entanto, alguns estudos demonstram que, mesmo ao adotar a mesma estrutura, soluções obtidas por meio da minimização de custos de transporte nem sempre são equivalentes às soluções obtidas pela minimização das emissões de CO₂ em redes logísticas mais complexas (por exemplo, intermodais).
7.2.2.1. Modelos Analíticos e Contínuos
Começamos discutindo o estudo de Bouchery e Fransoo (2015) sobre o projeto de redes intermodais no hinterlândia. Os autores apresentam um modelo analítico cujo objetivo é determinar a localização ótima de uma instalação (no exemplo deles, um terminal de contêineres no interior) considerando três objetivos: custo, emissões de carbono e mudança modal.
A demanda é assumida como uniforme sobre uma região retangular, que representa o hinterlândia do porto em consideração. A densidade da demanda é igual a contêineres por quilômetro quadrado, e a origem dos fluxos (o porto) está localizada nas coordenadas (0,0).
O modelo assume que custos de transporte e emissões de carbono possuem a mesma estrutura e considera duas opções de transporte: envio direto (transporte via caminhão diretamente da origem ao cliente) e transporte intermodal (envio via trem para um terminal intermodal e, posteriormente, transporte via caminhão do terminal até o cliente).
Os custos e emissões de CO₂ ao atender uma região de demanda i de tamanho Ai por envio direto são expressos como Z0,iDS = δ0,i ρ Ai Z1 e E0,iDS = δ0,i ρ Ai E1, onde:
= distância do porto ao centro de gravidade da zona de demanda (km)
= custo do transporte rodoviário por contêiner-quilômetro
= emissões de carbono do transporte rodoviário (kg de CO₂ por contêiner-quilômetro)
Os custos e as emissões de CO₂ quando se utiliza transporte intermodal são expressos da seguinte forma: Z0,jIT = δ0,T (ZF2 + ρ Ai Z2) + δT,i ρ Ai Z1 e E0,iIT = δ0,T (EF2 + ρ Ai E2) + δT,i ρ Ai E1, onde:
= distância do porto até o terminal intermodal no interior (km)
= distância do terminal até o centro de gravidade da zona de demanda i (km)
= custo fixo do transporte ferroviário por km
= custo variável do transporte ferroviário por contêiner-quilômetro
= emissões fixas associadas ao transporte ferroviário (kg de CO₂ por km)
= emissões lineares do transporte ferroviário (kg de CO₂ por contêiner-quilômetro)
Os autores identificaram soluções ótimas com base em dados europeus. Seus resultados mostram que o terminal intermodal está localizado mais próximo do porto quando a otimização é baseada em custo e mais distante do porto quando a otimização é baseada em emissões de carbono. Esse resultado demonstra que, mesmo quando custos e emissões de CO₂ possuem a mesma estrutura, há diferenças significativas nas soluções ótimas para ambas as formulações.
Esse efeito é explicado pelas diferenças nos parâmetros fixos do transporte ferroviário, o que também é consistente com o fato de que o transporte ferroviário sob alta utilização é mais eficiente em termos de emissões do que o transporte rodoviário, mas é mais caro em termos de custo. Para mais detalhes, referimo-nos ao estudo completo (Bouchery e Fransoo, 2015).
Embora outros artigos sobre modelos contínuos de localização de instalações verdes possam ser encontrados na literatura, a área ainda é pouco explorada. Buyuksaatci e Esnaf (2014) apresentam um problema de localização de instalações baseado em emissões de carbono, considerando a minimização das emissões de CO₂ utilizando o método do centro de gravidade. O estudo emprega uma formulação baseada no GHG Protocol, mas não discute nenhum insight gerencial ou implicação derivada da formulação proposta.
7.2.2.2. Modelos Discretos
Agora discutimos estudos sobre modelos de localização de instalações verdes com formulações discretas.
Diabat e Simchi-Levi (2010) apresentam um problema de localização de instalações de múltiplos níveis e múltiplas commodities com restrição de carbono. O objetivo do problema é determinar a localização ótima de fábricas e centros de distribuição, bem como a atribuição de fluxos, de forma a minimizar os custos totais sem exceder um limite máximo de emissões de carbono.
O modelo assume emissões de carbono na distribuição baseadas em um fator de emissão por distância percorrida (toneladas de CO₂ por km), negligenciando o impacto da carga transportada nas emissões de CO₂ (ver Capítulo 5 de Blanco e Sheffi, 2024). Apesar dessa simplificação grosseira, a conclusão geral segue uma lógica intuitiva: quanto menor a tolerância às emissões de carbono, maior o custo da cadeia de suprimentos.
Elhedhli e Merrick (2012) estudam um problema de projeto de redes de cadeia de suprimentos que considera as emissões de CO₂. O objetivo do estudo é minimizar simultaneamente os custos logísticos e os custos ambientais das emissões de CO₂, determinando estrategicamente a localização de armazéns dentro da rede de distribuição.
O modelo utiliza a estimativa do GHG Protocol para emissões de CO₂ e emprega um parâmetro de conversão para transformar as emissões de CO₂ em custo monetário. Essa abordagem permite incorporar o custo das emissões de carbono no projeto da rede de suprimentos. Os resultados experimentais demonstram que a inclusão dos custos de carbono leva a soluções em que mais centros de distribuição são abertos, reduzindo as emissões de CO₂ no transporte.
Embora o estudo forneça insights gerenciais interessantes, o modelo adota métodos agregados para estimar as emissões de CO₂ no transporte, como o GHG Protocol com fatores de emissão da EPA. Velázquez-Martínez et al. (2014a) abordam os efeitos de diferentes níveis de agregação na medição das emissões de carbono do transporte e demonstram que erros associados à agregação podem ser substanciais e sistemáticos. Isso sugere que o aumento do nível de detalhamento nos problemas de localização de instalações é necessário.
O custo pode não ser o único fator para reduzir as emissões de CO₂ no transporte. Por exemplo, as empresas podem estar sujeitas a sistemas de cap-and-trade ou podem utilizar a redução das emissões de carbono como um fator estratégico para gestão de marca, diferenciação de produto ou motivação de funcionários (CDP, 2011a, b). Isso sugere que uma formulação prática para modelos de localização de instalações verdes deve considerar simultaneamente os objetivos de custo e emissões de CO₂.
Uma possível alternativa para considerar ambos os objetivos (custo e emissões de CO₂) é modelar o problema de localização de instalações verdes em um contexto multiobjetivo. A maioria dos problemas do mundo real envolve naturalmente múltiplos objetivos (minimização de custos, maximização do nível de serviço, minimização das emissões de CO₂, etc.).
A abordagem multiobjetivo permite definir um conjunto de soluções eficientes (ou fronteira de Pareto), que representa o conjunto de soluções onde nenhuma solução pode ser melhorada em um critério sem piorar outro (Coello, 2009). Essas soluções eficientes são frequentemente preferidas em comparação com soluções únicas, pois são mais adequadas a problemas reais, nos quais a decisão final sempre envolve um trade-off (Konak et al., 2006).
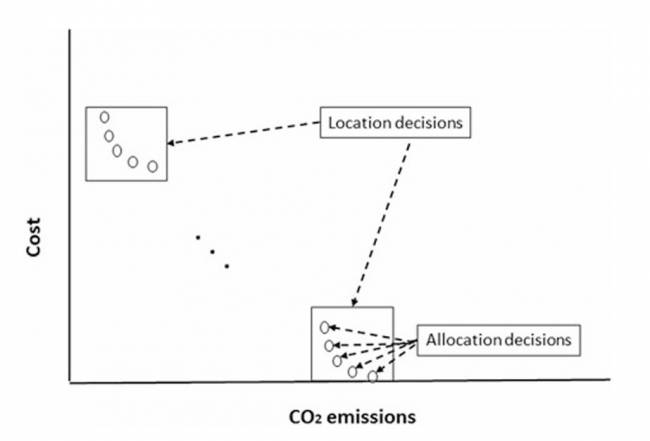
Seguindo essa linha de pesquisa, Harris et al. (2014) apresentam uma formulação do problema de localização de instalações com custo fixo (P3) com duas funções objetivo: custo e emissões de CO₂. O modelo de localização de instalações assume depósitos individuais com capacidades bj, onde cada cliente é atendido diretamente por um único depósito, garantindo que a condição de fonte única seja respeitada no modelo. Dessa forma, é possível construir um algoritmo de solução que primeiro determina quais instalações serão abertas e, em seguida, aloca os clientes às instalações abertas. O estudo propõe uma expressão para estimar as emissões de CO₂ do transporte baseada no GHG Protocol, ou seja, as emissões de CO₂ do transporte são linearmente dependentes da distância percorrida e da demanda. O estudo discute um método de otimização multiobjetivo para o modelo de localização de instalações com custo e CO₂, no qual o tomador de decisão pode explorar soluções de trade-off para a alocação de clientes com base na localização das instalações pré-selecionadas.
A Figura 7.2 (Harris et al., 2014) apresenta diferentes soluções para a decisão de localização e, para cada decisão, a possível alocação dos clientes.
O artigo foca nos métodos de solução e fornece um framework para analisar trade-offs entre custo e emissões de CO₂ em modelos de localização de instalações.
Como todos os estudos anteriores concluíram que o aumento no número de instalações abertas implica uma redução nas emissões de CO₂ do transporte (e, tipicamente, mais instalações também implicam em custos mais elevados), podemos argumentar que uma abordagem prática para analisar o trade-off entre custo e emissões de CO₂ na localização de instalações é simplificar a formulação ao não incluir as emissões fixas por instalação aberta.
Portanto, estamos interessados em estudar o efeito do custo de transporte versus as emissões de CO₂ do transporte considerando um número fixo de instalações previamente definido (ou seja, o problema p-Mediana).
Velázquez-Martínez et al. (2014b) analisam o trade-off entre custo e emissões de CO₂ utilizando uma abordagem multiobjetivo para o problema de localização de instalações. O modelo corresponde ao problema p-Mediana, com funções objetivo para custo e emissões de CO₂.
As suposições gerais do problema p-Mediana se aplicam a esse modelo, ou seja, a demanda é determinística e os locais candidatos são conhecidos previamente. Além disso, o modelo também assume que a empresa pode gerenciar múltiplos caminhões de diferentes capacidades e que os caminhões são atribuídos com base em restrições nos nós de demanda (ou na política da empresa). Essas suposições permitem que o modelo inclua a possibilidade de que certos clientes só possam ser atendidos por certos tipos de caminhões, cada um com estruturas de custo distintas.
Para formular a função objetivo de emissões de carbono, os autores incorporam a metodologia NTM na função objetivo (Velázquez-Martínez et al., 2014b).
Note que hi/Wi representa o número de viagens necessárias para atender o cliente i ∈ I e, portanto, afeta a distância total percorrida:
$$ l \sum_{j \in J} \sum_{i \in I} d_{ij} \left[ f_i^e \left\lfloor \frac{h_i}{W_i} \right\rfloor + \left( f_i^f - f_i^e \right) \frac{h_i}{W_i} \right] Y_{ij} $$
Essa formulação permite entender em mais detalhes o trade-off entre a distância percorrida (dij) e a taxa de utilização (hi/Wi) ao decidir a alocação de instalações.
Por exemplo, ao atender clientes com uma frota homogênea (ou seja, Wi = W para todo i ∈ I), as soluções de localização são as mesmas obtidas pelo modelo P1, ou seja, as instalações são localizadas próximas aos clientes com maior demanda. Nesse caso, minimizar o custo de transporte é equivalente a minimizar as emissões de CO₂.
Entretanto, ao atender clientes com uma frota não homogênea (por exemplo, devido a restrições de caminhões impostas por regulamentações ou infraestrutura de transporte), as instalações podem ser localizadas mais próximas de clientes atendidos por caminhões menores. Isso pode ser explicado pelo fato de que esses clientes exigem múltiplas viagens e, portanto, uma distância maior é percorrida para atendê-los, aumentando as emissões de CO₂.
7.3. Implicações Práticas dos Modelos de Localização Verde
O transporte é um dos principais fatores contribuintes para as emissões globais de carbono e, portanto, ao lidar com modelos de localização de instalações em um contexto de distribuição, as emissões do transporte podem ser substancialmente maiores do que as emissões provenientes da produção ou do armazenamento. Além disso, como os modelos de localização de instalações definem a configuração das entregas, os modelos de localização verde tornam-se uma alternativa importante para a redução das emissões de CO₂ na logística. Como o transporte geralmente está incluído no Escopo 3 do inventário de GEE e costuma representar a maior fonte de emissões em uma cadeia de suprimentos, as empresas podem começar a focar mais no aumento do número de centros de distribuição para melhorar o alcance aos clientes. Esse fenômeno tem sido observado nos maiores varejistas, como a Amazon, como resultado do modelo de negócios de entrega rápida e da necessidade de aumentar a velocidade do atendimento ao cliente (Dastin, 2020).
Enquanto as soluções de minimização de custos tendem a localizar instalações mais próximas de clientes com alta demanda, as soluções de minimização das emissões de CO₂ tendem a posicionar instalações mais próximas de clientes que possuem restrições de acessibilidade para caminhões. Isso ocorre porque as restrições de caminhões aumentam o número de viagens necessárias para atender aos clientes, e esse fator tem um impacto maior do que o crescimento da demanda e/ou da utilização dos veículos. Esse aspecto pode ser particularmente importante para empresas que gerenciam frotas não homogêneas ou para políticas públicas em áreas densamente povoadas, onde a demanda é elevada (devido à alta densidade populacional e à presença de pequenas lojas), mas veículos pesados não são permitidos. Novas regulamentações podem ser necessárias para equilibrar a acessibilidade de caminhões grandes em determinados períodos, a fim de aumentar a eficiência logística e reduzir o número de veículos pequenos nessas regiões.
Para alguns problemas logísticos, mesmo quando abordagens agregadas são utilizadas para estimar as emissões de CO₂ do transporte e, portanto, a formulação compartilha a mesma estrutura dos custos de transporte, as soluções de localização podem ser substancialmente diferentes. Para empresas interessadas em aumentar a mudança modal ou em utilizar mais transporte intermodal, essas estratégias podem resultar em um aumento nas emissões de CO₂. Em especial, quando diferentes modais são utilizados, como em redes intermodais, as diferenças nos parâmetros de custo de transporte e emissões de CO₂ podem levar a um conjunto completamente diferente de soluções para ambas as funções objetivo.
Um modelo multiobjetivo para os modelos de localização verde pode fornecer aos tomadores de decisão um framework para analisar o trade-off entre custo e emissões de CO₂. Essa abordagem pode oferecer uma nova ferramenta para as empresas definirem estratégias mais eficazes para a redução das emissões de CO₂. Como os tomadores de decisão provavelmente buscam alternativas que reduzam as emissões sem aumentar excessivamente os custos, a modelagem multiobjetivo proporciona um conjunto de soluções de trade-off que não eram conhecidas em modelos com um único objetivo. Isso pode implicar no surgimento de novas soluções equilibradas entre custo e emissões de CO₂. Por exemplo, localizações com pequenos aumentos de custo podem gerar grandes reduções nas emissões de CO₂.
7.4. Direções para Trabalhos Futuros
A área de localização de instalações verdes ainda é pouco explorada na pesquisa. Como os custos de transporte e as emissões de CO₂ não possuem a mesma estrutura, uma formulação específica para a minimização das emissões de CO₂ em modelos de localização de instalações deve ser considerada. Infelizmente, poucos estudos utilizam expressões detalhadas para estimar as emissões de CO₂ no transporte em modelos de localização. A maioria das pesquisas se baseia no GHG Protocol e no GLEC Framework, o que significa que o efeito completo das emissões ainda não foi totalmente estudado e compreendido.
Além disso, poucas empresas implementaram estratégias que utilizam a localização de instalações para reduzir seu impacto ambiental. Portanto, mais aplicações dos modelos em casos práticos são necessárias, de modo que a compreensão e a validação dos modelos e seus trade-offs possam ser aprofundadas na prática.
Outro aspecto pouco abordado na literatura é a inclusão das emissões geradas pelas próprias instalações nas formulações dos modelos. Quando isso é considerado, geralmente apenas a geração de eletricidade é levada em conta. Os modelos são, em sua maioria, focados nas emissões provenientes do transporte, especialmente na última milha. No entanto, nenhuma pesquisa foi conduzida para analisar o impacto do transporte de matérias-primas na localização de instalações. Dessa forma, novas formulações de modelos são necessárias para preencher essa lacuna.
Neste capítulo, limitamos nossa discussão ao impacto das emissões de carbono provenientes de fontes móveis. No entanto, considerar diferentes fontes de energia para as instalações (eólica, combustíveis, etc.) e incluí-las em modelos futuros de localização de instalações verdes para entender o impacto das fontes energéticas na escolha das localizações planejadas representa uma promissora linha de pesquisa. Isso se torna especialmente relevante em conexão com a estratégia de eletrificação do setor de transporte.
As instalações podem desempenhar um papel fundamental no suporte ao transporte eletrificado, funcionando como pontos de armazenamento de baterias elétricas ou outras fontes de energia, bem como atuando como hubs energéticos para fornecimento de carga e estações de recarga.
Referências
Akçelik R, Besley M (2003) Operating cost, fuel consumption, and emission models in aaSIDRA and aaMOTION. In: 25th Conference of Australian Institutes of Transport Research (CAITR 2003). University of South Australia, Adelaide, Australia
Balinski ML (1965) Integer programming: methods, uses, computation. Manag Sci 12:253–313 Blanco EE, Sheffi Y (2024) Green logistics. In: Bouchery Y, Corbett CJ, Fransoo JC (eds)
Sustainable supply chains: a research-based textbook on operations and strategy. Springer, Cham
Bouchery Y, Fransoo JC (2015) Cost, carbon emissions and modal shift in intermodal network design decisions. Int J Prod Econ 164:388–399
Boukherroub T, Bouchery Y, Tan T, Fransoo J, Corbett C (2024) Carbon footprinting in supply chains: measurement, reporting and disclosure. In: Bouchery Y, Corbett CJ, Fransoo JC (eds) Sustainable supply chains: a research-based textbook on operations and strategy. Springer, Cham
Buyuksaatci S, Esnaf S (2014) Carbon emission based optimization approach for the facility location problem. Online J Sci Technol 4(1)
Campbell JF (2013) A continuous approximation model for time definite many-to-many transportation. Transp Res B Methodol 54:100–112
Carlsson JG, Jia F (2013) Euclidean hub-and-spoke networks. Oper Res 61:1360–1382 CDP (2011a) Carbon disclosure project. Available on www.cdproject.net/.
CDP (2011b) Carbon disclosure project. Supply chain report: ATKearney. Available at https://www.cdproject.net/CDPResults/CDP-2011-Supply-Chain-Report.pdf.
Cholette S, Venkat K (2009) The energy and carbon intensity of wine distribution: a study of logistical options for delivering wine to consumers. J Clean Prod 17(16):1401–1413
Christou IT (2011) Coordination of cluster ensembles via exact methods. IEEE Trans Pattern Anal Machine Intell 2:279–293
Coello CA (2009) Evolutionary multi-objective optimization: some current research trends and topics that remain to be explored. Front Comput Sci China 3(1):18–30
Daskin MS (2008) What you should know about location modeling. Wiley Periodicals
Daskin MS, Dean L (2005) Location of health care facilities. Oper Res Health Care J 70:43–76


















